class Node { int data; Node left; Node right; public Node(int data, Node left, Node right) { this.data = data; this.left = left; this.right = right; } } class BinarySearchTree { Node head; public BinarySearchTree(int data) { this.head = new Node(data, null, null); } public void addNode(int data) { Node cur = this.head; Node parent = cur; while (cur != null) { if (data == cur.data) { System.out.p..
자료구조 & 알고리즘
// 각각의 엣지에 가중치가 있는 포화 이진 트리가 있다. // 루트에서 각 리프까지의 경로 상 가중치 합을 각각 같게 하고, // 모든 가중치들의 총합이 최소가 되도록 하는 프로그램을 작성하세요. - 포인트 1. 엣지를 트리로 보기 - 포인트 2. 후위 순회하기.. - 포인트 3. 차이를 더해주기 ==> += Math.abs(x - y); - 포인트 4. 높이로 포화이진트리 담을 배열의 길이 구하기 --> 정답 풀이 케이스에서 활용 ==> Math.pow(2, h + 1); public class MyCode { // 후위 순회 --> 트리 문제 풀때 무슨 순회인지 먼저 파악하기 ! public static void solution(int h, int[] w) { // 후위 순회.. // 엣지를 노드..
class Node { char data; Node left; Node right; Node(char data, Node left, Node right) { this.data = data; this.left = left; this.right = right; } } class BinaryTree2 { Node head; BinaryTree2(char[] arr) { // 배열로 노드 구성한 후, 링크트 리스트 엮는 방식 -> 노드를 idx로 접근... Node[] nodeList = new Node[arr.length]; // 노드타입 배열 먼저 구성하기 !! for (int i = 0; i < nodeList.length; i++) { nodeList[i] = new Node(arr[i], null, n..
주어진 인덱스가 idx 일 때 ( 수정 필요..?) 부모 노드의 인덱스 : idx = (idx / 2) - 1; 왼쪽 자식 노드의 인덱스 : idx = idx * 2 + 1; 오른쪽 자식 노드의 인덱스 : idx = idx * 2 + 2; - 재귀적으로 호출하여 출력하는 구조 주의 ! - 전위 순회 : 먼저 출력 (preOrder) - 중위 순회 : 중간에 출력 (inOrder) - 후위 순회 : 마지막에 출력 (postOrder)class BinaryTree { char[] tree; BinaryTree(char[] arr) { tree = arr.clone(); } public void preOrder(int idx) { // 전위 순회 int left = idx * 2 + 1; int right =..
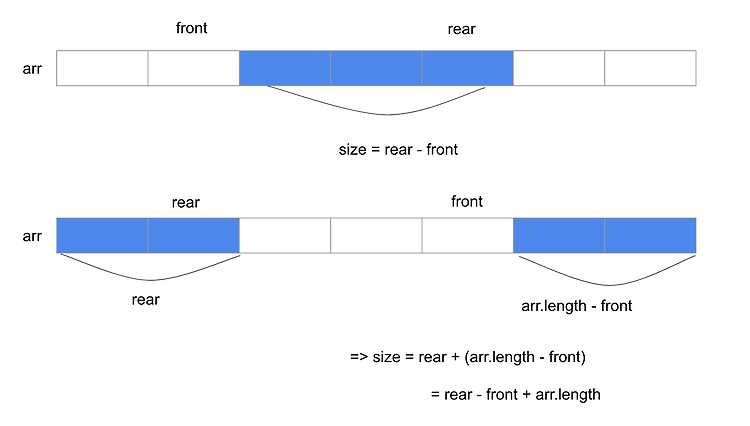
이번 게시물은 제가 좋아하는 유튜버(간다효)처럼 제목을 지어봤습니다. 원형큐에서 큐의 길이를 구할 때는 두가지 경우로 나눠서 생각해봐야 합니다. 1. front가 앞에, rear가 뒤에 있는 상황 2. rear가 앞에, front가 뒤에 있는 상황 소스코드로 나타내면 이렇게 볼 수 있는데요, int size; if (rear - front < 0) { size = rear - front + arr.length; } else { size = rear - front; } 공식처럼 생각하면 그렇구나, 하고 넘어갈 수 있지만 .. 머리속으로 떠올리면 또 쉽게 이해가 되지 않아서.. 직접 그려보았습니다.. rear - front가 음수일 경우는 rear가 배열의 앞쪽에, front가 배열의 뒷쪽에 위치한 상태로 ..
알고리즘 문제를 풀다가 헷갈리는 상황이 생겼습니다.. 링크드 리스트, 큐, 데크 등의 선형 자료구조의 이미지를 떠올릴 때.. 어디가 앞이고 어디가 뒤인 거지? (front) LIST (last) //..? 혹은 (last) LIST (front) // 어디가 front야..? 위 상황에서 보통 add()와 addLast()라는 메소드가 있으니까.. 두 메소드는 반대의 기능을 하는걸까...? add-->> (front) LIST (last) (front) LIST (last) (last) LIST (front) (last) LIST (front) (front) LIST (rear) (front) LIST (rear) 4 [1, 2, 3] deque.removeFirst() ==> 1 [2, 3] deque..
- 원형 데크 구현 예시 템플릿 // 배열을 이용한 기본 데크 직접 구현 class MyDeque { MyDeque(int size) { } public boolean isEmpty() { } public boolean isFull() { } public void addFirst(int data) { } public void addLast(int data) { } public Integer removeFirst() { } public Integer removeLast() { } public void printDeque() { } } public class Practice2 { public static void main(String[] args) { // Test code MyDeque myDeque = ..
- 원형 큐 구현 예시 템플릿 class MyQueue { MyQueue (int size) { } public boolean isEmpty() { } public boolean isFull() { } public void enqueue(int data) { } public Integer dequeue() { } public void printQueue() { } } class MyQueue { int[] arr; //배열로 만든 원형큐에서 front는 항상 비워둔다 int front; int rear; MyQueue(int size) { //front를 비워두므로 길이 + 1 arr = new int[size + 1]; front = 0; rear = 0; } public boolean isEmpty(..